算法10.矩阵相交 |

普通分析

算法

发布日期: 2020-10-02

更新日期: 2020-10-02

文章字数: 948

阅读次数:

题目描述

平面上有两个矩形A和B，其位置是任意的。编程求出其相交部分（即重叠部分）的面积。（0<a，b<1000）

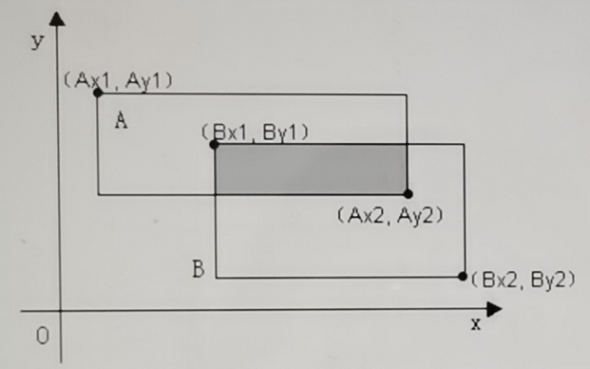
从标准输入读取两行以空格分隔的整数，格式如下：
Ax1 Ay1 Ax2 Ay2
Bx1 By1 Bx2 By2

其中（x1，y1）为矩形一个顶点座标，（x2，y2）为前一顶点的对角顶点座标。各座标值均为整数，取值在0至1000之间。

向标准输出打印一个整数，是两矩形相交部分的面积（可能为0）。在输出末尾要有一个回车符。

示例 1：

输入:  0 0 2 2
      1 1 3 4
输出: 1

解题思路

方法：普通分析

时间复杂度：$O(1)$

空间复杂度：$O(1)$

代码如下

#include <math.h>
#include <stdio.h>

int main(){
    int Ax1,Ay1,Ax2,Ay2,Bx1,By1,Bx2,By2,s;
    scanf("%d %d %d %d", &Ax1,&Ay1,&Ax2,&Ay2);
    scanf("%d %d %d %d", &Bx1,&By1,&Bx2,&By2);
    int xA_min,xB_min,xA_max,xB_max,yA_min,yB_min,yA_max,yB_max;

    // 确定A矩阵横纵坐标的最大最小值
    xA_min = Ax1<Ax2?Ax1:Ax2; xA_max = Ax1>Ax2?Ax1:Ax2; yA_min = Ay1<Ay2?Ay1:Ay2; yA_max = Ay1>Ay2?Ay1:Ay2;
    // 确定B矩阵横纵坐标的最大最小值
    xB_min = Bx1<Bx2?Bx1:Bx2; xB_max = Bx1>Bx2?Bx1:Bx2; yB_min = By1<By2?By1:By2; yB_max = By1>By2?By1:By2;
    // 排除相离相切情况
    if(xB_max<=xA_min || xA_max<=xB_min || yB_max<=yA_min || yA_max<=yB_min){
        printf("0\n");
    }
    // 分析相交情况的阴影面积
    else
    {
        int sx1,sx2,sy1,sy2;
        // 求出横坐标最小值中的最大值
        if(xA_min<=xB_min)
            sx1 = xB_min;
        else
            sx1 = xA_min;
        // 求出横坐标最大值中的最小值
        if(xA_max<=xB_max)
            sx2 = xA_max;
        else
            sx2 = xB_max;
        // 求出纵坐标最小值中的最大值
        if(yA_min<=yB_min)
            sy1 = yB_min;
        else
            sy1 = yA_min;
        // 求出纵坐标最大值中的最小值
        if(yA_max<=yB_max)
            sy2 = yA_max;
        else
            sy2 = yB_max;

        s = (sy2 - sy1) * (sx2 - sx1);
        printf("%d\n",s);
    }


}

解法分析

这道题的关键点是划分好哪些情况矩阵是相离（或者相切），哪些情况矩阵是相交。

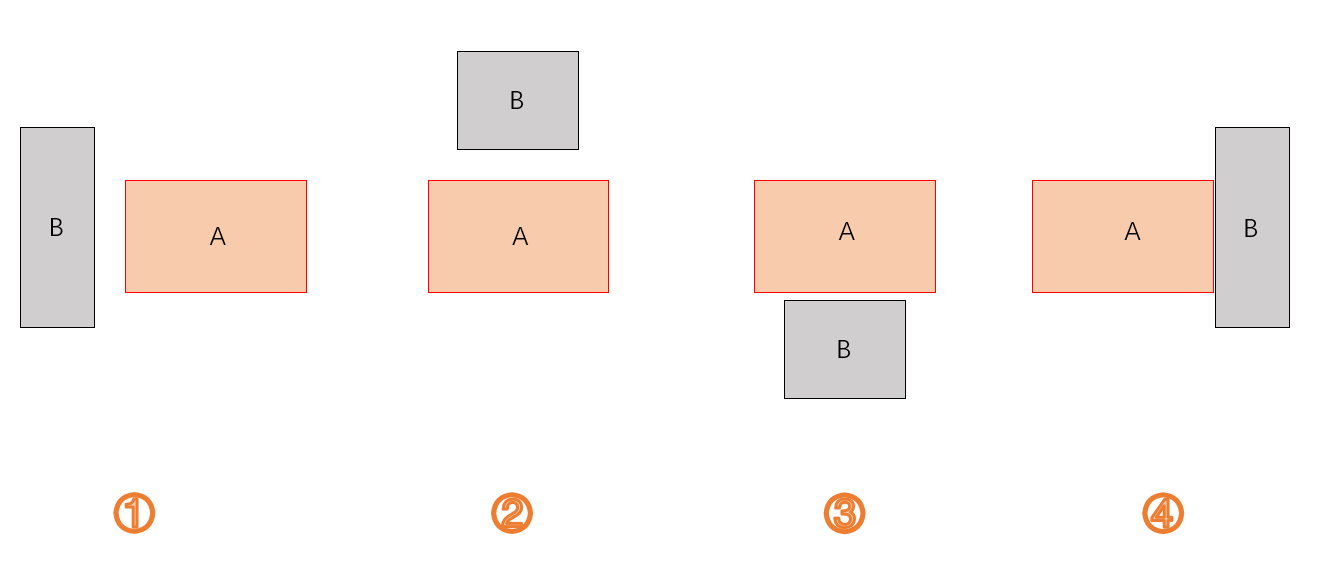
那么，两个矩阵怎样摆放才使得阴影面积为0呢？

假设A矩阵固定，有以下四种情况会使得阴影面积为0：

B矩阵的最大横坐标还没有A矩阵最小横坐标大
B矩阵的最小纵坐标还要比A矩阵最大纵坐标大
B矩阵的最大纵坐标还没有A矩阵最小纵坐标大
B矩阵的最小横坐标还要比A矩阵最大横坐标大

相应的图示情况如下：

不相交情况图示

题目给了我们四个点的坐标，两两顶点对角，我们先把每个矩阵的最小横坐标xA_min、xB_min，最大横坐标xA_max、xB_max，最小纵坐标yA_min、yB_min，最大纵坐标yA_max、yB_max求出来，接着就可以进行相交判断：

if(xB_max<=xA_min || xA_max<=xB_min || yB_max<=yA_min || yA_max<=yB_min){
    printf("0\n");
}

解决了相离相切情况之后，接下来探讨相交情况：

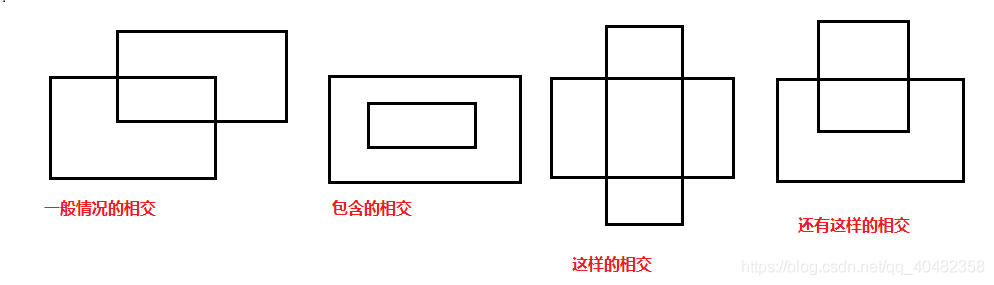
相交情况图示

乍一看感觉好像很复杂，但是仔细分析之后，其实还是有规律可循的。

可以看到，每次相交之后，阴影矩形的长总是由xA_max和xB_max中的最小值和xA_min和xB_min中的最大值的距离构成；同样地，阴影矩形的宽总是由yA_max和yB_max中的最小值和yA_min和yB_min中的最大值的距离构成。

把阴影面积的长宽求出来之后，就可以将最后的面积求出。

解法注意点