算法9.打印从1到最大的n位数

题目描述

输入数字 n，按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3，则打印出 1、2、3 一直到最大的 3 位数 999。

示例 1：

输入: n = 1
输出: [1,2,3,4,5,6,7,8,9]

解题思路

方法：DFS递归

时间复杂度：$O(10^n)$

空间复杂度：$O(10^n)$

代码如下

class Solution {
public:
    char digital[10] = {'0','1','2','3','4','5','6','7','8','9'};
    vector<int> res;
    int total_bits;
    char num[100];
    vector<int> printNumbers(int n) {
        total_bits = n;
        // num = new char[n];
        dfs(0);
        // delete[] num;

        res.erase(res.begin());
        return res;

    }
    void dfs(int index){
        if(index == total_bits){
            res.push_back(atoi(&num[0]));
        }
        else{
            for(int i=0; i<10; i++){
                num[index] = digital[i];
                dfs(index+1);
            }
        }
    }
};

解法分析

这道题乍一看很简单，题目也没有要求考虑大数条件。但如果考虑了大数条件，就会变得稍微复杂起来了。本题在考虑大数情况下，采用$DFS$递归，主要思路是先固定高位，向低位递归，当个位数被固定，再固定十位0~9，按顺序开启递归，直到到达最高位，终止递归。

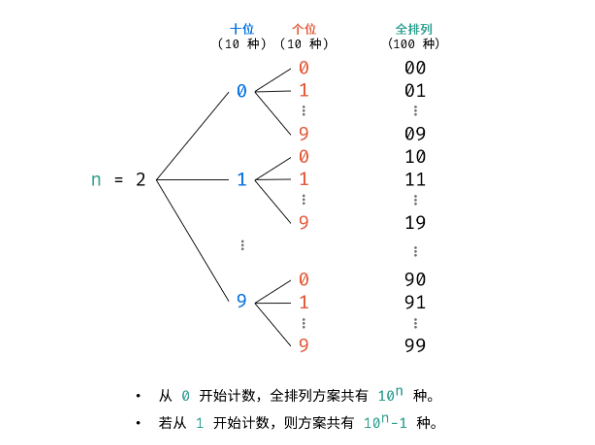
主要步骤

• 定义一个n位数的字符数组，用来存放最终结果。
• 先将所有要用到的数组或者变量放到全局中，以免递归的时候多次传递。
• 递归传入一个索引index，刚开始索引为0，待到索引为n的时候，结束本次递归。
• 对每一位按照0~9的顺序依次分配字符。

解法注意点

• 最后生成的字符串需要通过atoi函数变成整数。
• 去掉第一项（题目要求开头不为0）