算法7.剪绳子 |

算法

发布日期: 2020-09-26

更新日期: 2020-09-26

文章字数: 1.2k

阅读次数:

题目描述

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]...k[m-1] 。请问 k[0]*k[1]*...*k[m-1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

示例 1：

输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1

示例 2：

输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36

解题思路

方法一：动态规划(自底向上)

时间复杂度：$O(N^2)$

空间复杂度：$O(N)$

代码如下

class Solution {
public:
    int cuttingRope(int n) {
        int dp[n+1];
        for(int i=0; i<=n; i++){
            dp[i] = 0;
        }
        for(int i=1; i<=n; i++){
            for(int j=1; j<i; j++){
                dp[i] = max(dp[i],max(dp[j],j)*max(dp[i-j],i-j));
            }
        }
        return dp[n];
        // cout<<dp[n]<<endl;
    }
};

解法分析

绳子有着固定长度n，动态规划的思想就是把1~n-1的所有值都求出来放在一个数组里，通过前面这些值来求n的值。本题的思路也是这样的：

假设dp[n]代表绳子长度为n切出来乘积结果的最大值。那么求dp[n]的时候，每次都从1~n-1遍历一遍，将dp[n]分解成dp[i]和dp[n-i]的乘积，再比较遍历中的最大值。

解法注意点

因为本题要求绳子至少要切一次，所以无论绳子有多短（比如n=2），也要想办法切出来，即使最终的乘积比没切的时候还小。因此就会出现下列特殊情况：

n=2 dp[n]=1<2
n=3 dp[n]=2<3
n=4 dp[n]=4=4

举个例子，当n=8时，切成i=3和n-i=5时，dp[3]就不再是最优解了，因此这个时候应该停止切分dp[3]，所以在算法判别的时候，要加入max(dp[j],j)这个元素。

方法二：记忆化递归(自顶向下)

时间复杂度：$O(2^N)$

空间复杂度：$O(N)$ 若不用空间数组，则空间复杂度为$O(2^N)$

代码如下

class Solution:
    def cuttingRope(self, n: int) -> int:
        # 使用辅助函数
        def memoize(n):
            if n == 2: return 1
            if f[n] != 0: # 如果f[n]已经计算过，直接返回避免重复计算
                return f[n]
            res = -1
            for i in range(1, n):
                res = max(res, max(i * (n - i),i * memoize(n - i)))
            f[n] = res
            return res

        f = [0 for _ in range(n + 1)]
        return memoize(n)

解法分析

绳子有着固定长度n，动态规划的思想就是把1~n-1的所有值都求出来放在一个数组里，通过前面这些值来求n的值。本题的思路也是这样的：

递归图示

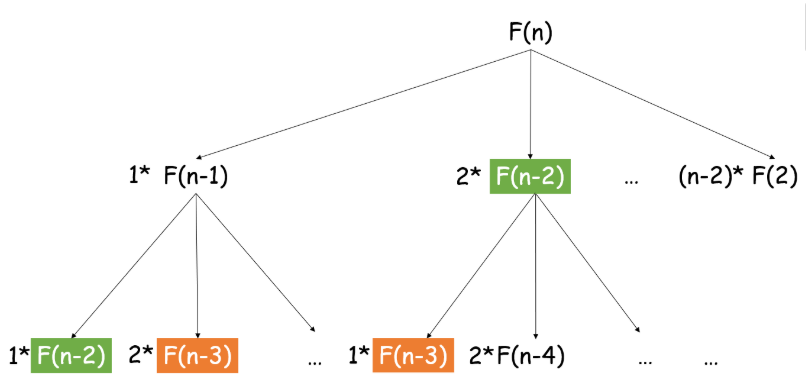
解法注意点

相比于不开数组直接递归，这种解法对空间和时间更友好一些。暴力解法会超时，但是很多进阶解法往往是暴力解法的优化。注意到上述代码中超时的原因主要是因为重复计算了 $F(n)$，为了避免重复计算可以使用记忆化技术。

记忆化技术的代码中经常需要建立函数 memoize 辅助实现。我们使用数组 f 来保存长度为 i时的最大长度 f[i]，最后返回 f[n]即可。

方法三：数学推导

时间复杂度：$O(1)$

空间复杂度：$O(1)$

代码如下

class Solution {
public:
    int cuttingRope(int n) {
        if(n==2||n==3)
            return n-1;
        if(n==4)
            return 4;
        if(n>4){
            long long int sum=1;
            while (n>4)
            {
                sum *= 3;
                sum %= 1000000007;
                n -= 3;
            }
            sum *= n;
            sum %= 1000000007;
            return sum;
        }
        else
        {
            return -1;
        }

    }
};