算法12.表示数值的字符串

题目描述

请实现一个函数用来判断字符串是否表示数值（包括整数和小数）。

示例 1：

输入:
+100 5e2 -123 3.1416 -1E-16 0123
输出: true

示例 2：

输入:
12e 1a3.14 1.2.3 +-5 12e+5.4
输出: false

解题思路

方法：普通分析

时间复杂度：$O(N)$

空间复杂度：$O(1)$

代码如下

//摘自LeetCode中Krahets大佬
class Solution:
    def isNumber(self, s: str) -> bool:
        states = [
            { ' ': 0, 's': 1, 'd': 2, '.': 4 }, # 0. start with 'blank'
            { 'd': 2, '.': 4 } ,                # 1. 'sign' before 'e'
            { 'd': 2, '.': 3, 'e': 5, ' ': 8 }, # 2. 'digit' before 'dot'
            { 'd': 3, 'e': 5, ' ': 8 },         # 3. 'digit' after 'dot'
            { 'd': 3 },                         # 4. 'digit' after 'dot' (‘blank’ before 'dot')
            { 's': 6, 'd': 7 },                 # 5. 'e'
            { 'd': 7 },                         # 6. 'sign' after 'e'
            { 'd': 7, ' ': 8 },                 # 7. 'digit' after 'e'
            { ' ': 8 }                          # 8. end with 'blank'
        ]
        p = 0                           # start with state 0
        for c in s:
            if '0' <= c <= '9': t = 'd' # digit
            elif c in "+-": t = 's'     # sign
            elif c in "eE": t = 'e'     # e or E
            elif c in ". ": t = c       # dot, blank
            else: t = '?'               # unknown
            if t not in states[p]: return False
            p = states[p][t]
        return p in (2, 3, 7, 8)

解法分析

因为数字的正确与否匹配一定的规则，所以可以利用有限状态机的原理解答这道题目。

首先进行状态定义：

开始状态

1. 开始的空格
2. 幂符号前的正负号
3. 小数点前的数字
4. 小数点、小数点后的数字
5. 当小数点前为空格时，小数点、小数点后的数字
6. 幂符号
7. 幂符号后的正负号
8. 幂符号后的数字
9. 结尾的空格

结束状态

• 合法的结束状态有 2, 3, 7, 8。

接着对可能的输入做一些分类

可能的输入有：

1. 数字（0-9）
2. 正负号（+-）
3. e（或者E）
4. 小数点（.）
5. 其他符号

对每个状态所有可能达到的状态进行分析

分析图如下：

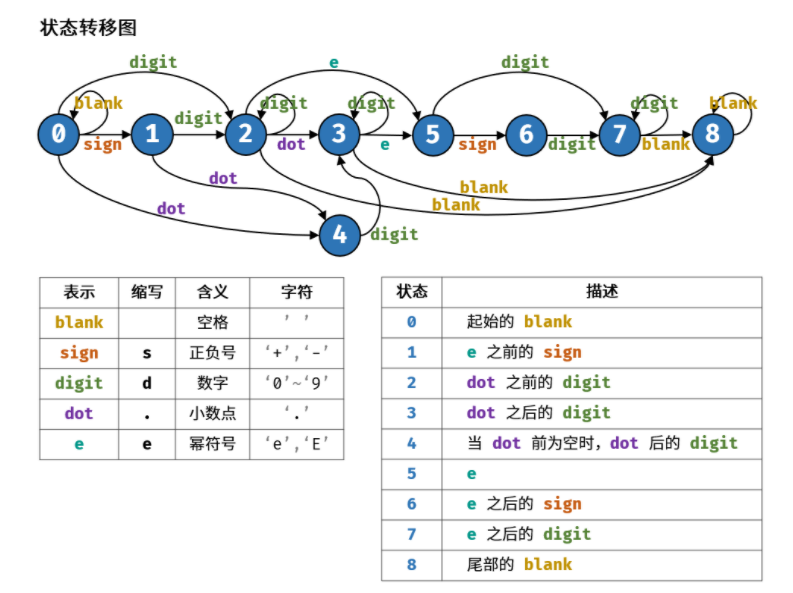
终止条件

若字符类型 $t$ 不在哈希表 $states[p]$ 中，说明无法转移至下一状态，因此直接返回 $False$ 。
状态转移： 状态 $p$ 转移至 $states[p][t]$ 。

返回

跳出循环后，若状态 $p∈2,3,7,8$ ，说明结尾合法，返回 $True$ ，否则返回 $False$ 。