算法5.旋转数组的最小数字

题目描述

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个递增排序的数组的一个旋转，输出旋转数组的最小元素。例如，数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一个旋转，该数组的最小值为1。

示例 1：

输入：[3,4,5,1,2]
输出：1

示例 2：

输入：[2,2,2,0,1]
输出：0

解题思路

方法：二分法

时间复杂度：$O(log_2n)$ 若数组中所有元素都相同，则退化到$O(N)$

空间复杂度：$O(1)$

代码如下

class Solution {
public:
    int minArray(vector<int>& numbers) {
        int start = 0;
        int end = numbers.size()-1;
        int mid;
        while (start < end)
        {
            mid = (start + end) / 2;
            if(numbers[mid] > numbers[end])
                start = mid+1;
            else if(numbers[mid] < numbers[end])
                end = mid;
            else 
                end--;
        }
        cout<<numbers[start]<<endl;
        return numbers[start];   
    }
};

解法分析

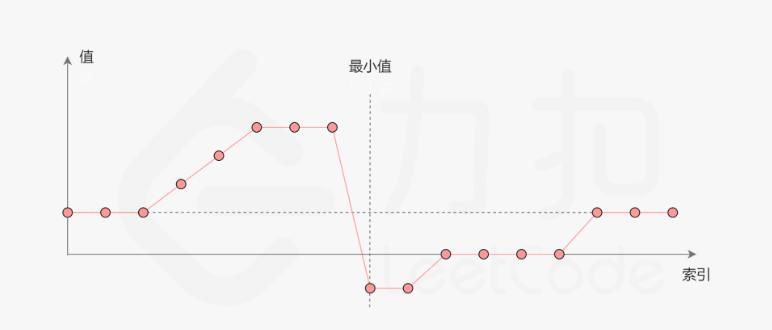
如上图所示，由于旋转，数组呈两次递增状态，最低点夹在中间。通过二分法可以判定出最低点的位置。具体判定如下：

设start=0，end=size()-1

• 当mid所处的值大于start所处的值时，证明最低点在右边，因此二分法取后者
• 当mid所处的值小于start所处的值时，证明最低点在左边，因此二分法取前者
• 当数组所有元素都是同一个值时，上述方法不再试用，二分法相当于遍历了一遍数组。

解法注意点

主要在于当mid所处的值等于start所处的值时，要怎么去处理二分法。上述代码是将end往前移动了一位。其形式相当于遍历。从代码量来说，不失为一种好方法。